Performance

This page presents various performance tests to evaluate the performance of SPMF.

2018-02-20 Which high-utility itemset mining algorithm is the most efficient ? (part 2)

A very detailled performance comparisonof high utility itemset mining algorithms, with the implementations of SPMF, was published by Chongsheng Zhang, George Almpanidis, Wanwan Wang, Changchang Lithat in a paper in Expert Systems with Applications (2018). The article compares the performance in terms of memory consumption and execution time of the following algorithms including: EFIM, d2HUP, UPGrowth, IHUP, Two-Phase, HUI-Miner, FHM, ULB-Miner and mHUI-Miner.

From a quick read of the paper, I have noted some interesting facts reported by the authors. In terms of execution time, EFIM and D2HUP are generally the two fastest algorithms and which one is faster depends on database characteristics. EFIM is faster on dense datasets, while D2HUP is faster on sparse and large databases. In terms of memory EFIM is on overall the most memory efficient algorithms. Some recent algorithms like ULB-Miner and mHUI-Miner on overall do not better than EFIM and D2HUP. And the older algorithms like IHUP, Two-Phase and UPGrowth are not competitive at all with newer algorithms in terms of speed.

Comments by Philippe: I had a quick look at the paper. This paper is a very detailled investigation and provides very interesting insights on the behavior of these algorithms. It is by far the most detailled comparison of high utility itemset mining algorithms. Below, I will provide a few comments that may be interesting.
(1) About the EFIM algorithm, one of the conclusion is that transaction merging is less effective on sparse datasets. To increase the performance, it is possible to deactivate transaction merging. In the EFIM paper of 2016, it was actually found that this can increase performance by up to 5 to 10 times on some sparse datasets.
(2) Using synthetic dataset is important to evaluate algorithms as it allows to check the influence of database characteristics. However, I am wondering whether the fact of using synthetic datasets might have a negative influence on some algorithms. For example, consider EFIM. Since synthetic datasets are randomly generated, it seems possible that the number of identical transactions may be less in random datasets than in real datasets, and thus that fewer transactions may be merged. Random datasets may also have a negative influence on the performance of other algorithms like FHM that rely on the fact that some item co-occurr more often together.
(3) Based on the paper, it would be possible to design a meta-algorithm that would select an appropriate algorithm based on dataset characteristics. And this could also be extended to select appropriate optimizations for each algorithm.

2015-09-01 Which high-utility itemset mining algorithm is the most efficient ? (part 1 - updated)

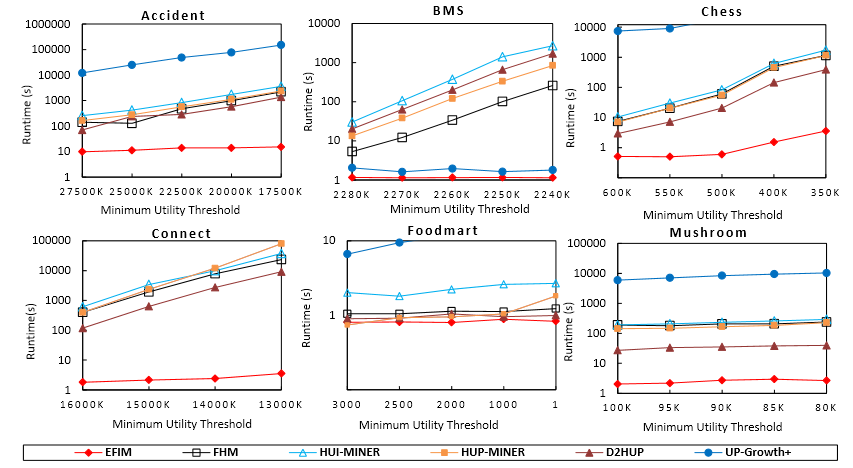
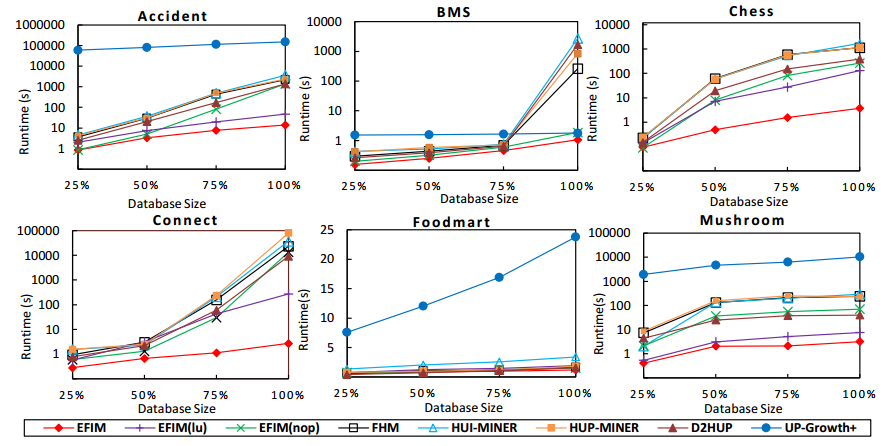
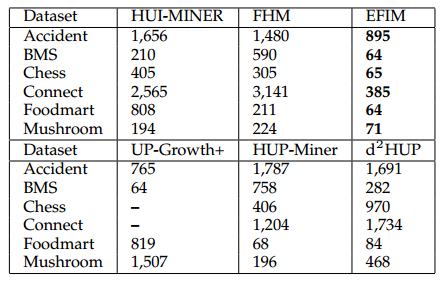
In SPMF 0.97, a highly-efficient algorithm for mining high-utility itemsets was introduced named EFIM (Zida et al., 2015). Here is a performance comparison with the state-of-the-art algorithms for high-utility itemset mining. In this comparison, EFIM is compared with two versions of EFIM without optimizations and several state-of-the-art algorithms, on common datasets used in the litterature for evaluating such algorithms. It can be seen that EFIM is up to three orders of magnitude faster than the other algorithms and use up to eight times less memory. Moreover, it can be seen that it also has better scalability. See the EFIM paper for more details about these experiments.

Execution time comparison

In this experiment, the minutil threshold is varied on a set of benchmark datasets. It can be observed that EFIM is up to three orders of magnitude faster than previous state-of-the-art algorithms.

Scalability Comparison

We also performed a scalability experiment where we varied the number of transactions for each dataset while setting the minutil parameter to the lowest value used in the previous experiment. The goal is to observe the influence of the number of transactions on execution. Results are shown below. It can be observed that EFIM has the best scalability.

Maximum Memory Usage Comparison

Here a comparison of memory usage (in megabytes) is performed for the lowest minutil value in the first experiment. It can be observed that EFIM has a very low memory consumption compared to other algorithms.

2015-09-01 Performance Comparison of On-Shelf High-Utility Itemset Mining Algorithms

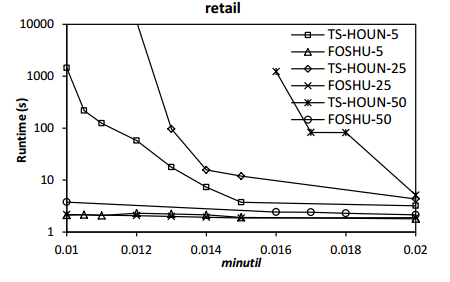
In SPMF 0.97, algorithms have been added for the problem of on-shelf high utility itemset mining. Here is a comparison of the performance of the FOSHU (Fournier-Viger, 2015) and TS-HOUN (Lan et al., 2014) algorithm, on various datasets commonly used in the litterature. In these experiments the minutil threshold is varied to see the influence on execution time. Moreover, the number of periods is also varied (5, 25 and 50 periods).It can be seen that FOSHU clearly outperform TS-HOUN on all datasets and also is more scalable w.r.t the number of time periods. See the FOSHU paper for more details about these experiments.

Comparison of execution time with respect to the minutil threshold

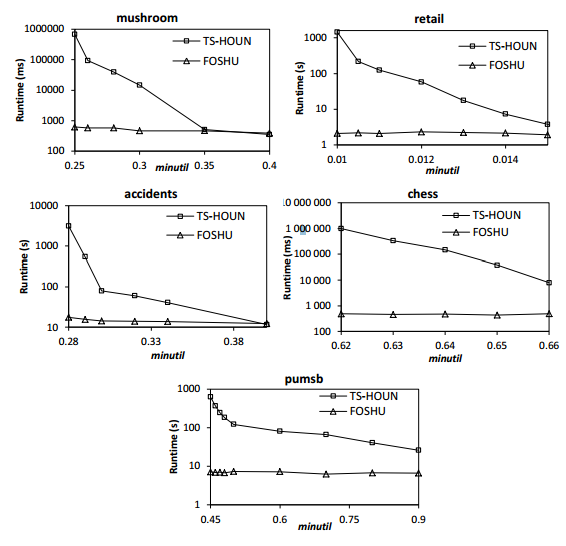
Comparison of execution time with respect to the the number of time periods

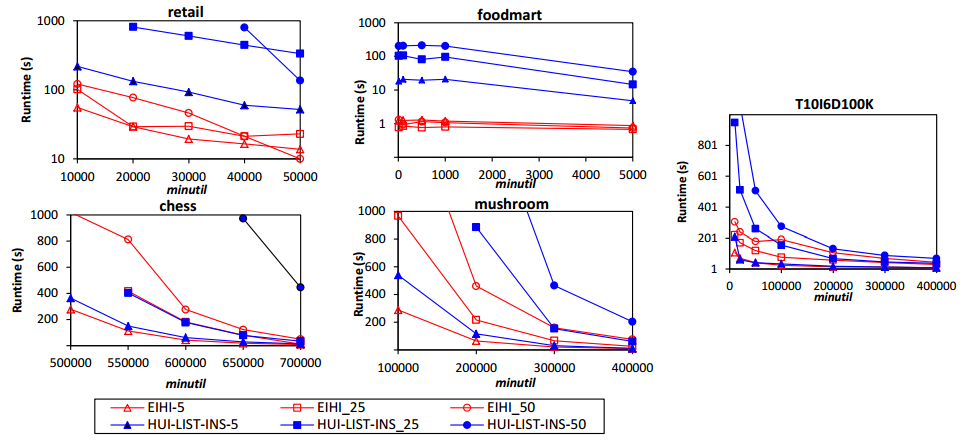
2015-09-01 Performance Comparison of Incremental High-Utility Itemset Mining Algorithms

In SPMF 0.97, implementations of two incremental high-utility itemset mining algorithms named HUI-LIST-INS and EIHI where added. Here is a comparison of their execution time with respect to the minutil threshold. Moreover, for each algorithm, a different number of updates was performed for each database (5, 25 and 50). It can be seen that EIHI is up to two orders of magnitude faster and more scalable with respect to the number of updates. See the EIHI paper for more details about those experiments.

2014-03-06 Which high-utility itemset mining algorithm is the most efficient ?

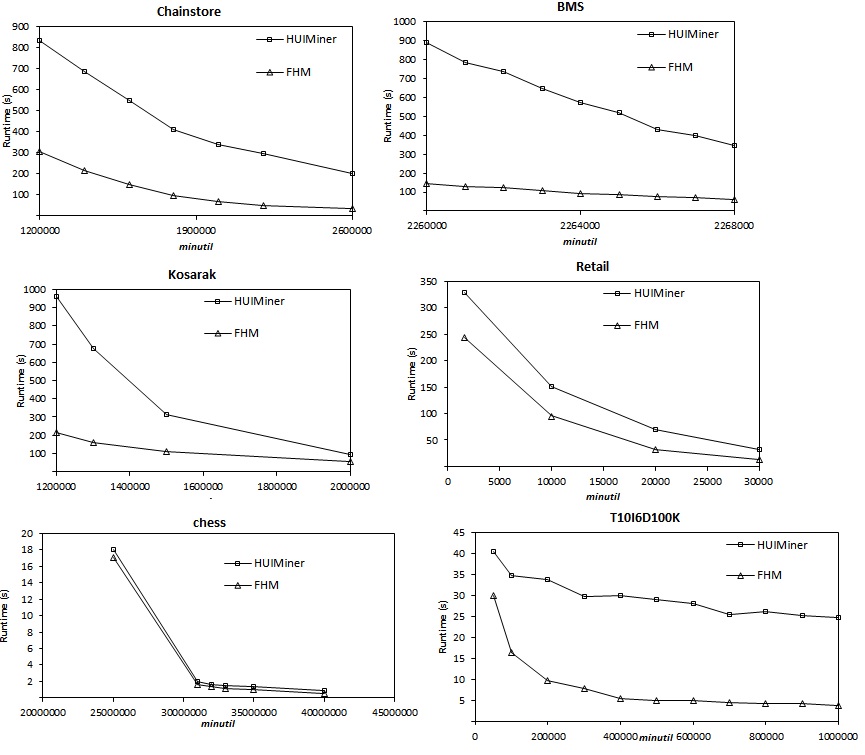
In SPMF 0.96, a novel algorithm named FHM is introduced for high utility itemset mining
(Fournier-Viger, June 2014 / March 2014 on the SPMF website).

In this experiment, we compare its performance with HUI-Miner, the state-of-the-art algorithm for high-utility itemset mining presented at CIKM 2012. We have performed an experiment on six datasets and measured the execution time. Most of the datasets can be found on the "datasets" page of this website. In conclusion, we can see that FHM is up to six times faster than HUI-Miner for most datasets. However, for very dense datasets such as Chess, both algorithms have similar behavior.

2014-06: SPMF (0.96f) vs. Coron (0.8): Eclat, Charm, Apriori, AprioriClose, AprioriRare...

We present new results of experiments to compare the performance of some algorithm implementations in SPMF with implementations in other data mining library. Previously, we had compared the performance of the SPMF implementation of FPGrowth with that of Weka. In this experiment, we compare the performance of SPMF with another Java data mining library named Coron (v.0.8). Note that unlike SPMF, Coron is not open-source and Coron cannot be used in commercial software.

Experimental setup

For the experiments, we have chosen four popular datasets used in the pattern mining literature (Chess, Accidents, Connect and Retail), which have varied characteristics. The datasets can be downloaded freely from the the "datasets" section of the SPMF website.

A computer with 5 GB of free RAM and a core i5 3th generation processor was used, running Windows 7. Cygwin was used to launch Coron since it requires to use SH scripts that cannot be run directly on Windows (note that we also tried running SPMF from Cygwin and it does not make a significant difference). For recording the running time of Coron, we use the "time" command of Cygwin. We also configured coron so that it would save the result to a file just like SPMF does, so that the time for writing to the disk would be considered for both implementations. For example, to run the Eclat algorithm in Coron and calculate the execution time and save the result to a file, we used the command: time ./core01_coron.sh connect.basenum 60% -alg:eclat -of:output.txt -vc:tm.

The goal of the experiments was to measure the execution time when the "minsup" threshold parameter was lowered.

We compared 8 algorithms that are common between SPMF and Coron: Eclat, Charm, Apriori, AprioriClose, AprioriRare, Zart, generate all association rules, generate closed association rules.

We did not compare the implementations of AprioriInverse since the Coron implementation does not offer both parameters minsup and maxsup that the algorithm should have, and the documentation of Coron does not explain why, while in SPMF both parameters can be set.

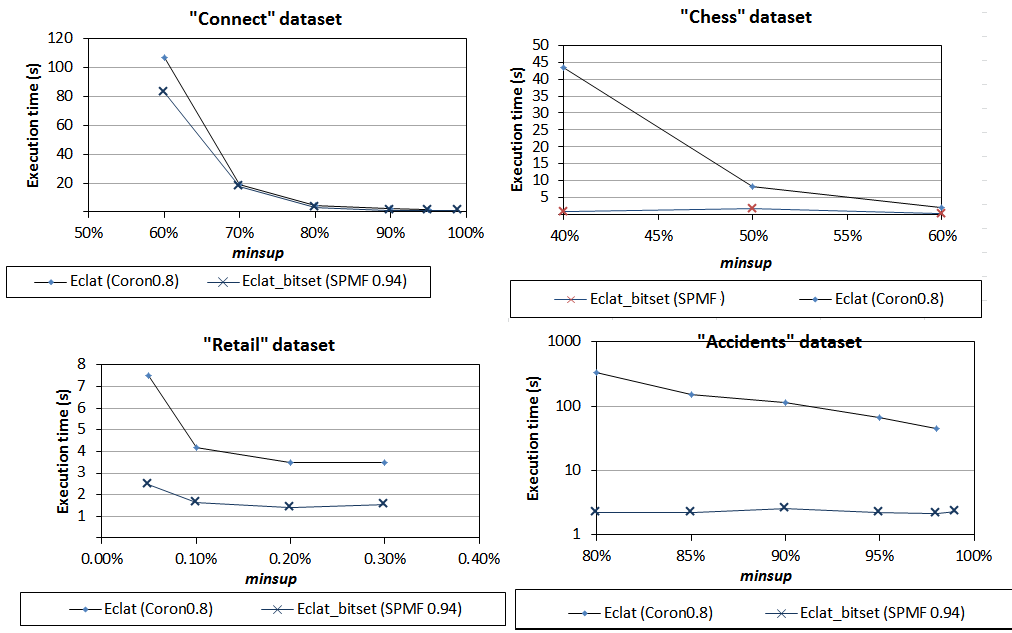
1) Comparison of Eclat implementations

We first compared Eclat implementations. For SPMF, the compared implementation is named Eclat_bitset. As we can see from the results below, the SPMF implementation of Eclat has the best performance on all datasets.

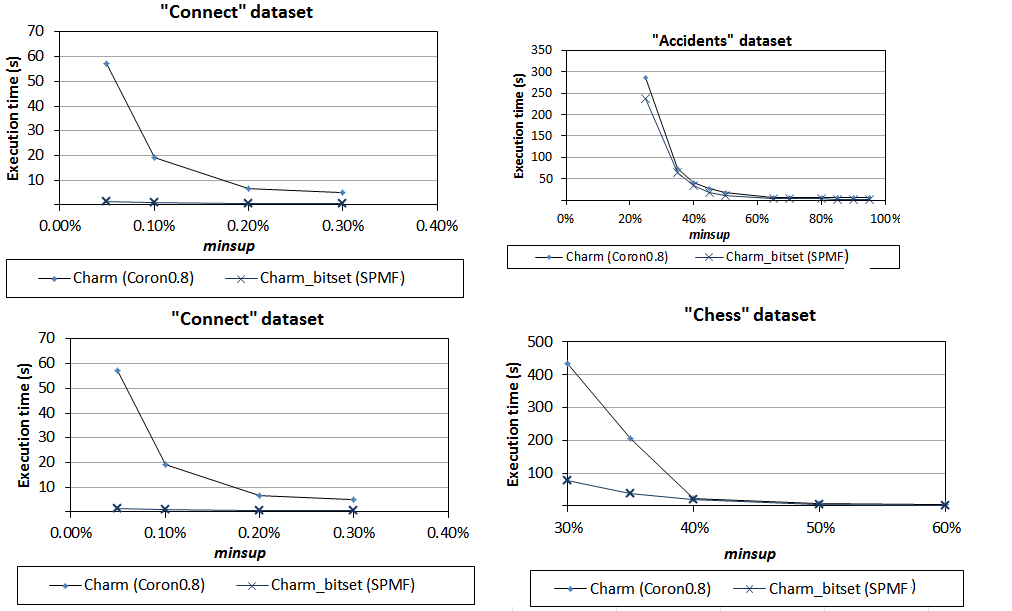
2) Comparison of Charm implementations

We have next compared Charm implementations. As we can see from the results below, the SPMF implementation has the best performance on all datasets.

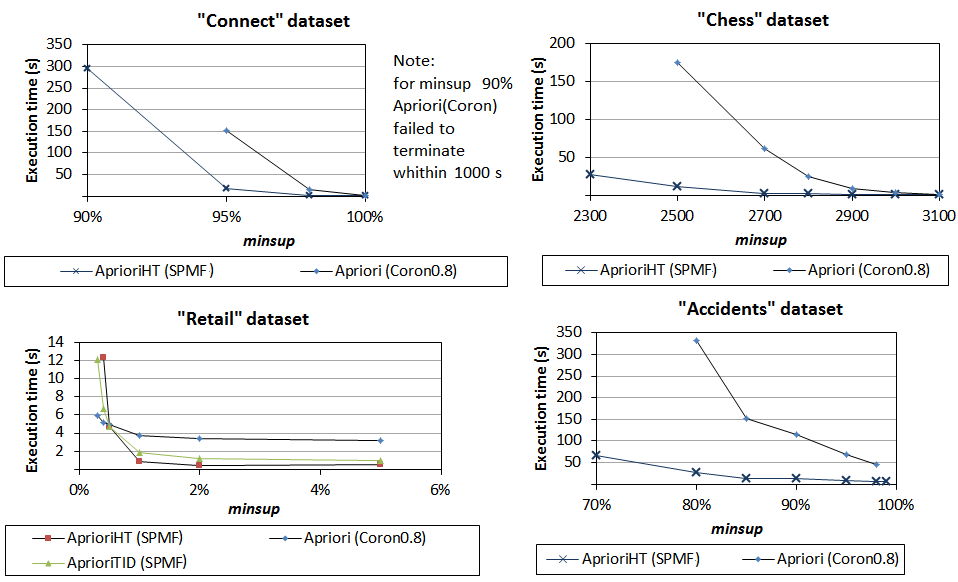
3) Comparison of Apriori implementations

We have next compared the Apriori implementations. In SPMF, we have used the best implementation named AprioriHT. As we can see, the SPMF implementation has the best performance on all datasets except Retail.

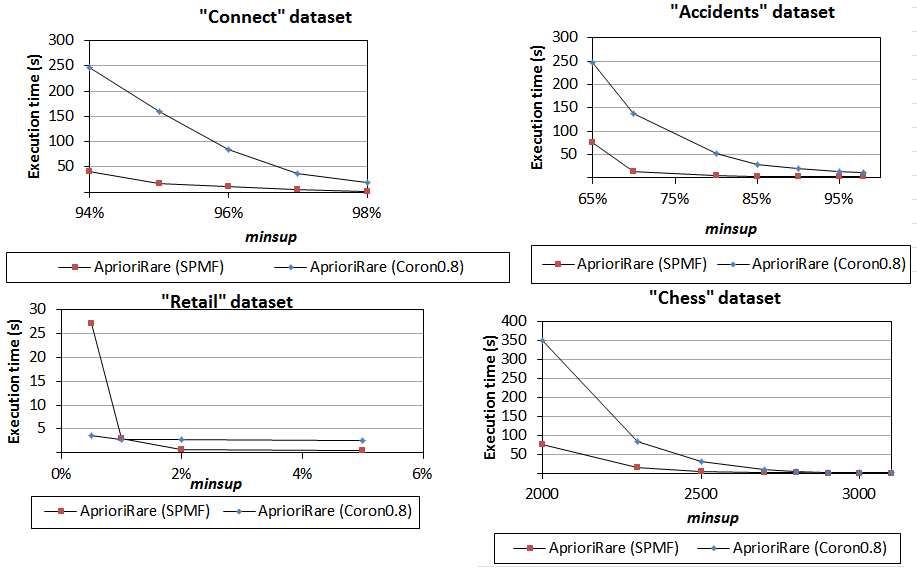
4) Comparison of AprioriRare implementations

We have next compared the AprioriRare implementations. As we can see, the SPMF implementation has the best performance on all datasets except Retail.

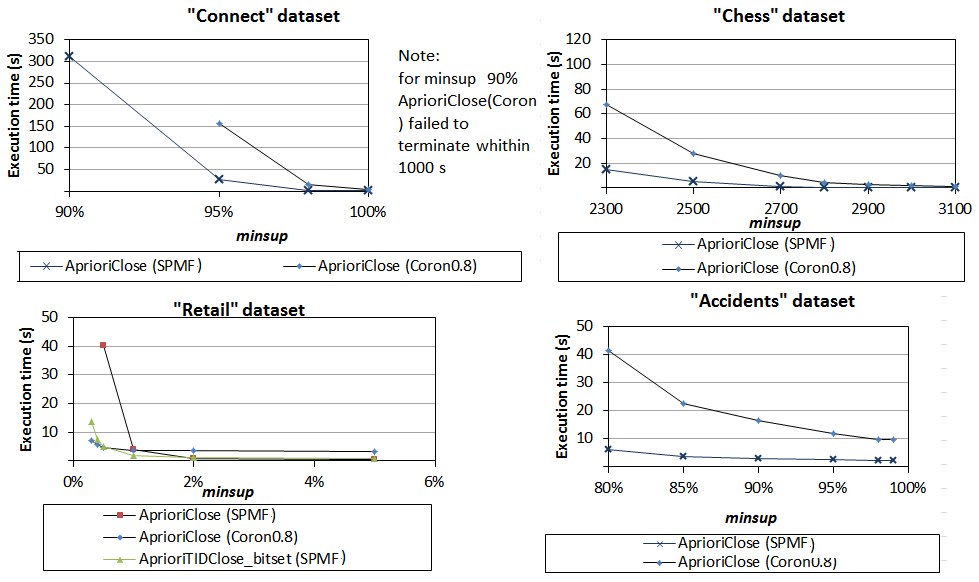
5) Comparison of AprioriClose implementations

We have next compared AprioriClose implementations. As we can see from the results below, the SPMF implementation has the best performance on all datasets except Retail.

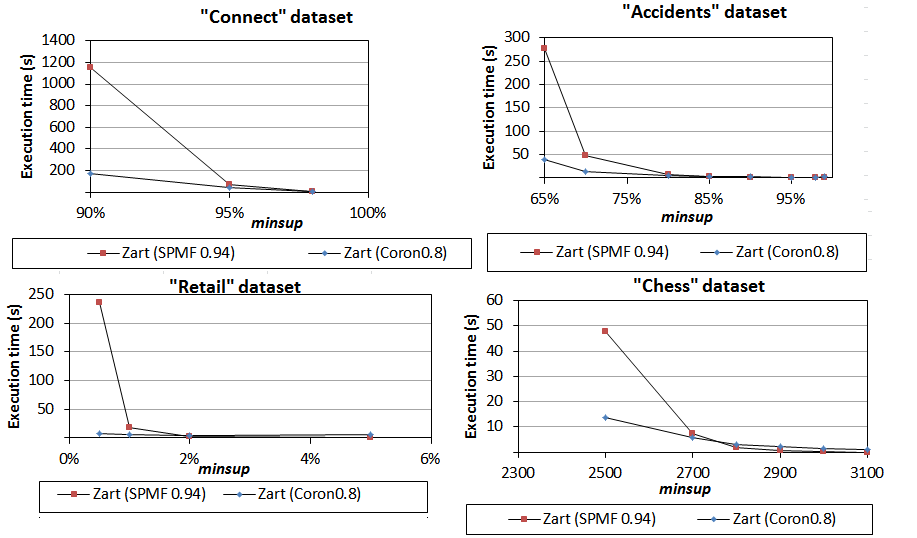
6) Comparison of Zart implementations

We have next compared the Zart implementations. In this case, the Coron implementation is clearly the best. The reason is that the implementation in SPMF of this algorithm is not optimized unlike most algorithms in SPMF. It could be improved in future work.

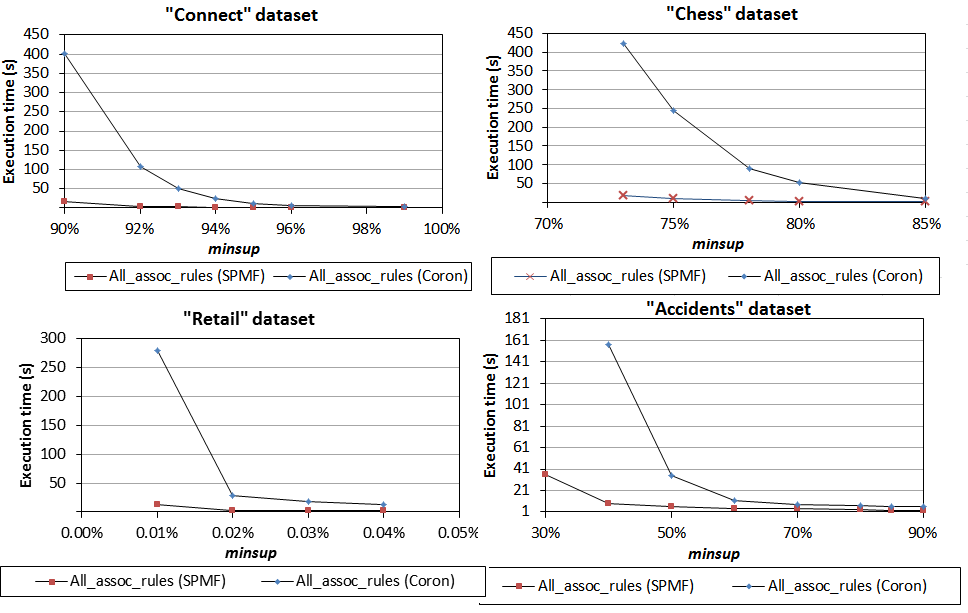
7) Comparison of time to discover valid association rules

We have next compared the total execution time for discovering the set of all valid association rules. Recall that association rule mining is performed in two steps : (1) discovering frequent itemsets and (2) generating rules using the frequent itemsets. The second step is always done using the algorithm of Agrawal. However the first step can in theory be done using any frequent itemset mining algorithms.

To perform the comparison of the total time for association rule generation, we choose to compare the best combination of algorithms for Step1+ Step2 respectively offered in SPMF and Coron for association rule generation. We thus used FPGrowth in Step1 for SPMF and Eclat for Step1 in Coron. Step 2 is then performed by the same algorithm both in Coron and SPMF. Note that FPGrowth is not implemented in Coron and that Eclat cannot be used for association rule generation in the current implementation of SPMF. Therefore, it was not possible to use exactly the same algorithm for this comparison. However, this comparison is still relevant because it shows how fast a user can get the set of all valid association rules using the best algorithms offered in each data mining library. Furthermore, after showing the results for Step1+Step2, we will break down the results into Step1 and Step2. Therefore, it will be possible to see the time for Step2 separately. For Step1, we had already compared Eclat implementations in another experiment.

Execution time of Step1 + Step 2. The total times are shown below for Step1+Step2 for Coron and SPMF on the same four datasets, when varying the minsup threshold and fixing the minimum confidence to 75 % (a typical value in the literature).

We conclude that it is much faster (up to 10 times faster) to discover all valid association rules using SPMF for these datasets, except for Retail where SPMF is still faster but the difference is smaller.

Execution time of Step 2. Following these results, we have examined the output to determine what is the bottleneck in terms of execution time for Coron. We determined that it is Step 2 rather than Step1. Although Step2 is performed by the algorithm of Agrawal (1993) both in Coron and SPMF, the execution time for Step2 in Coron is much slower than in SPMF. We illustrate this by breaking down the previous results into Step 1 and Step2:

• For the accidents dataset and minsup = 30 %,
  • Coron spend 5.8 s for Step1 (Eclat) and 14 minutes for Step2 (Agrawal93),
  • SPMF spend 8.5 s for Step 1 (FPGrowth) and 34.2 seconds for Step 2 (Agrawal93).
• For the chess dataset and minsup = 30 %,
  • Coron spend 0.4 s for Step1 (Eclat) and 7 minutes for Step2 (Agrawal93)
  • SPMF spend 0.1 s for Step 1 (FPGrowth) and 16 s for Step 2 (Agrawal93).
• For the connect dataset and minsup = 30 %,
  • Coron spend 1.3 s for Step1 (Eclat) and more than 6 minutes for Step2 (Agrawal93)
  • SPMF spend 0.8 s for Step 1 (FPGrowth) and 15 s for Step 2 (Agrawal93).
• For the retail dataset and minsup = 30 %,
  • Coron spend 46 s for Step1 (Eclat) and about 4 minutes for Step2 (Agrawal93)
  • SPMF spend 3.6 s for Step 1 (FPGrowth) and about 3 minutes for Step 2 (Agrawal93).

Execution time of Step 1. As previously said, we have compared in another experiment above the execution time of Eclat. So we will not discuss these results again. For FPGrowth, as said previously, it is not offered in Coron.

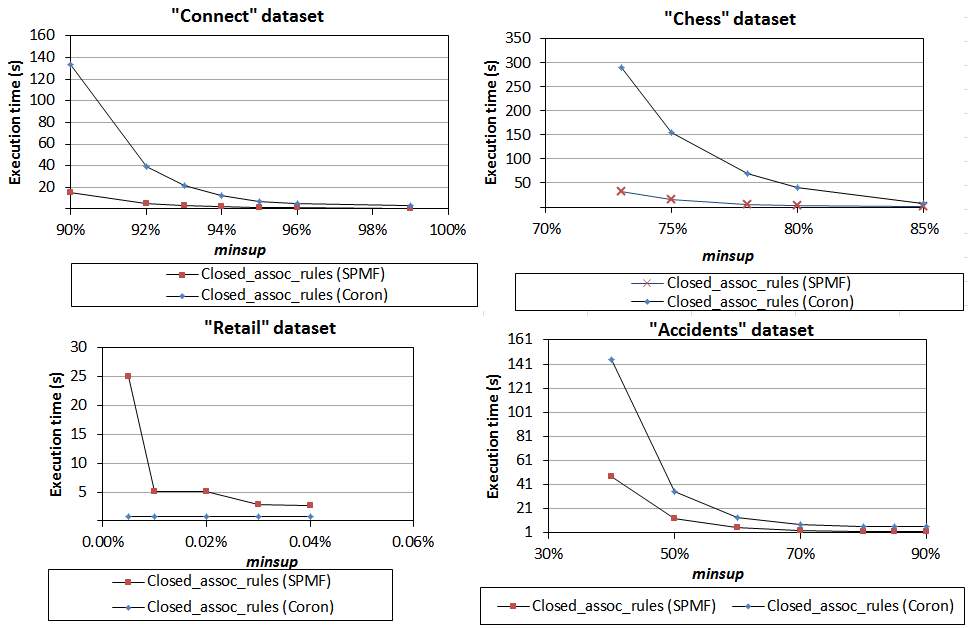
8) Comparison of time to discover closed association rules

We also did an experiment that is similar to the previous one but this time to generate CLOSED association rules. To do this, Step1 is the Charm algorithm and Step2 is an algorithm proposed by Szathmary. We also set minconf =0.75 and varied the minsup threshold to assess the execution on the same four datasets. Results shows that SPMF outperforms Coron for this task on three of the four compared datasets, although the difference of execution time is smaller than when generating all association rules in the previous experiment.

Note that for this experiment, we do not break down the results in Step1 and Step2 since Step1 is Charm for both SPMF and Coron and we have already compared the Charm implementations.

9) Conclusion of these experiments

We have observed that the implementations of the compared algorithms in SPMF are generally faster than the corresponding implementations in Coron under the parameters of our experiments (saving to file, using the four datasets, and varying minsup), except for the Zart algorithm because it has not been fully optimized in SPMF (this is something that we have on our "to-do list").

We have did our best to perform a fair experiment. However, since the source code of Coron is not open-source, it is not possible to analyze what design decisions lead to the performance that we have observed and what lesson learned could be used in SPMF. It is possible that Coron may be slower due to the way that it writes result to disk for example or because it performs additional pre-processing.

 

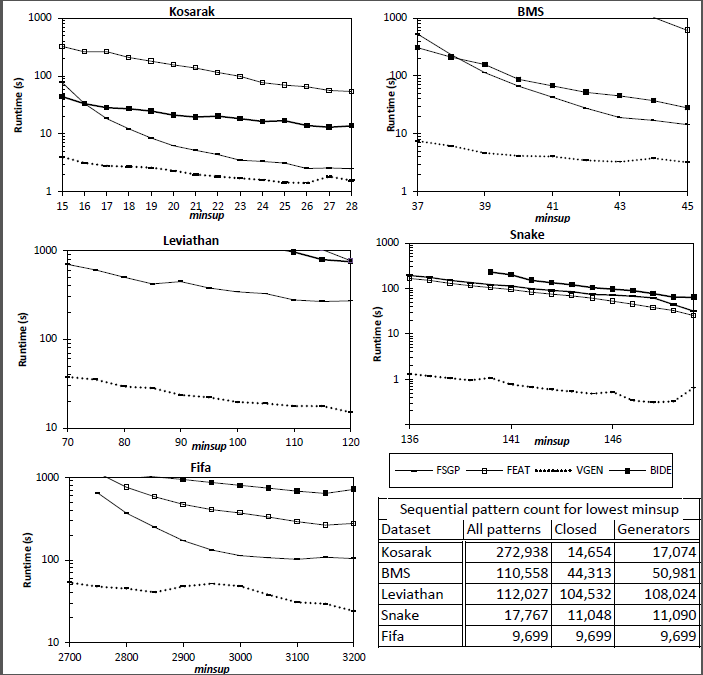
2014-05-21 Performance comparison of sequential generator pattern mining algorithms

In SPMF 0.96d, three algorithms have been introduced to mine sequential generator patterns: FEAT, FSGP and VGEN. In this experiments, we compare their execution times while varying the minsup parameter. We have used the Kosarak, BMS, Leviathan, Snake and FIFA datasets.

We have also included the BIDE algorithms for mining closed sequential patterns in the comparison since it was shown to be faster than the GenMiner algorithm (Lo et al., 2008) for sequential generator mining and we did not have the code of GenMiner. Furthermore, note that we did not compare with another algorithm named MSGP since it was reported to provide only a marginal improvement over the performance of FSGP (up to 10% - see Pham et al., 2012).

Results show that VGEN is up to two orders of magnitude faster than FEAT and FSGP.

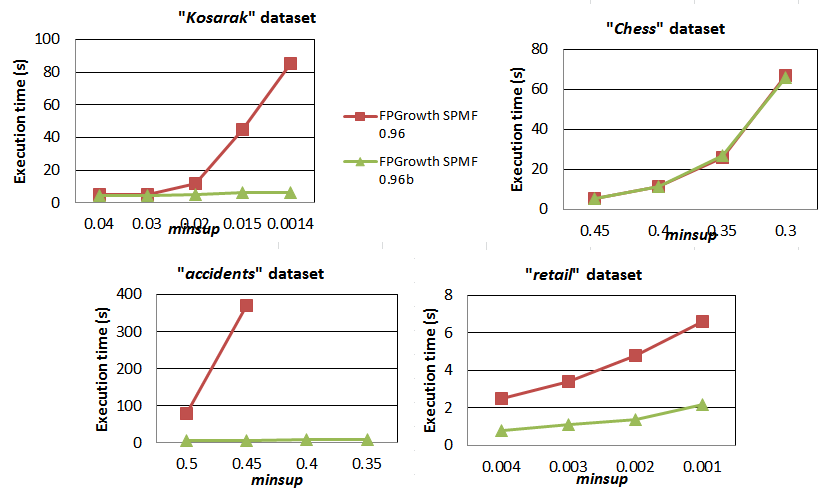
2014-04-29 Performance comparison of FPGrowth implementations of SPMF 0.96 and 0.96b

In SPMF 0.96b, an important optimizations of the SPMF FPGrowth implementation was performed. The modification is to add mapItemLastNodes in the FPTree / MISTree classes. We have performed a quick experiment on five popular transaction dataset by varying the "minsup" threshold to see the speed improvement. As it can be seen on the following charts, there is a huge improvement except for the "chess" dataset perhaps because this latter dataset is very dense and contains relatively few transactions.

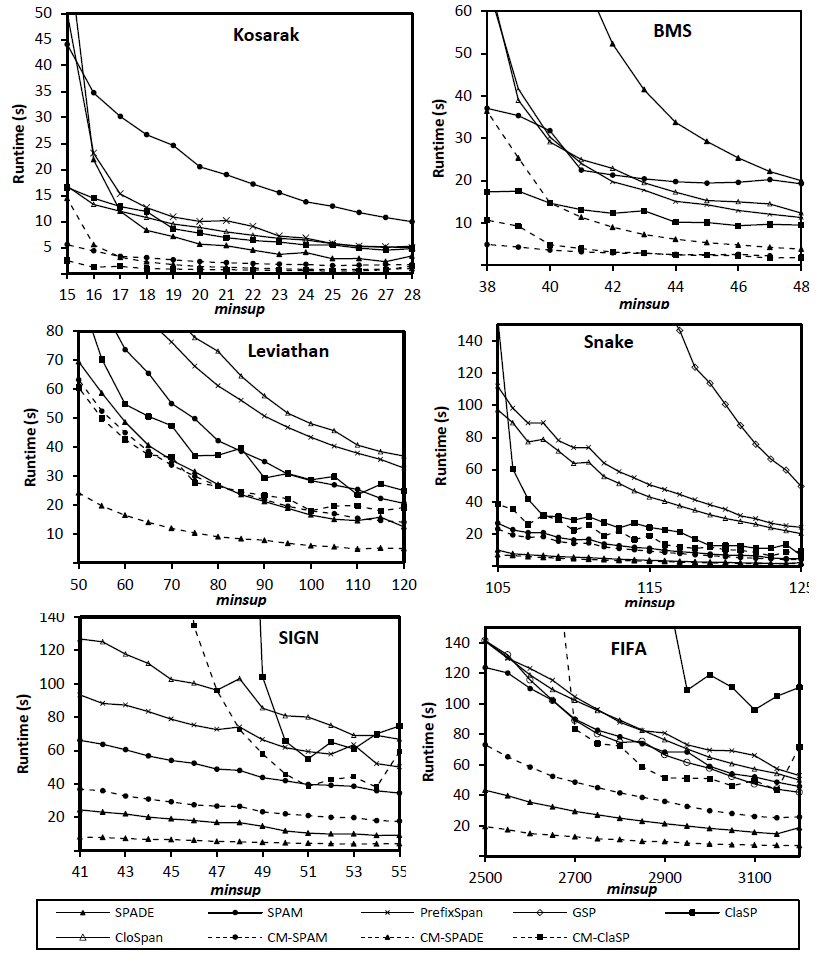
2014-02-28 Updated comparison of sequential pattern mining and closed sequential pattern mining algorithms (SPMF 0.95)

In SPMF 0.95, three new algorithm for sequential pattern mining have been added. Those are CM-SPAM, CM-SPADE and CM-ClaSP, which are optimization of SPAM, SPADE and Clasp by using a new strategy called co-occurrence pruning. We show below a comparison of the execution time of these algorithms against the SPADE, SPAM, PrefixSpan, GSP, Clasp and CloSpan algorithm for the Kosarak, BMS, Leviathan, Snake, SIGN and FIFA datasets. Those results are published in our PAKDD 2014 paper (Fournier-Viger et al., 2014).

For mining sequential patterns, CM-SPADE has the best performance on all but two datasets (BMS and Kosarak) where CM-SPAM is faster.

For mining closed sequential patterns, CM-ClaSP has the best performance on four datasets. For the other datasets, CloSpan is faster but for only low minimum support values. Note that in these experiments BIDE was not included for closed sequential pattern mining. But it did not had better performance than CloSpan and CM-ClaSP

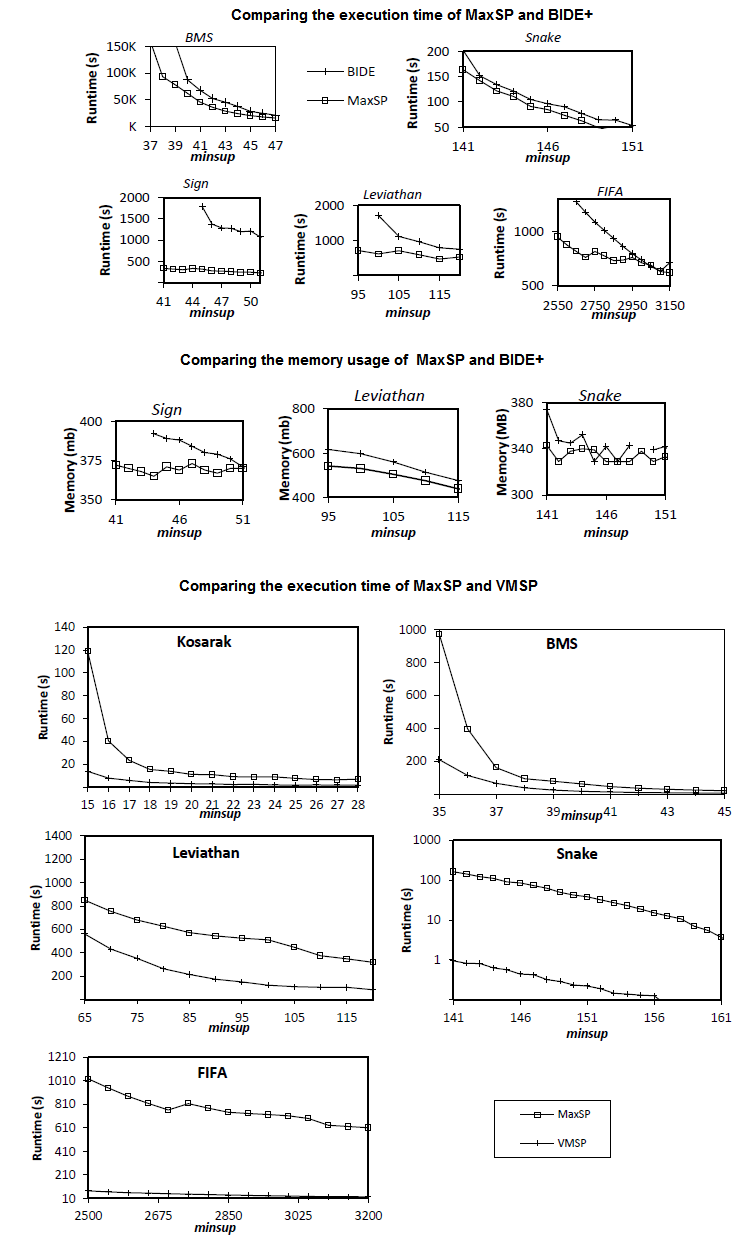
2013-02-28: Comparison of Maximal Sequential Pattern Mining Algorithms (SPMF 0.95)

In SPMF 0.95, we have added two new algorithms for discovering maximal sequential patterns named MaxSP and VMSP.

We have performed a comparison of the performance of MaxSP with BIDE+, an algorithm for closed sequential pattern mining because MaxSP is inspired by BIDE+ and we wanted to see if discovering maximal patterns would be faster.

Moreover, we have also compared the performance of MaxSP and VMSP to determine which algorithm is the best for discovering maximal sequential patterns.

Results are shown below. As it can be seen, MaxSP performs better than BIDE+, and VMSP performs better than MaxSP.

For more details about these results, please refer to the paper about VMSP and the paper about MaxSP.

2013-02-28: Comparison of Top-K Sequential Pattern Mining Algorithms (SPMF 0.95)

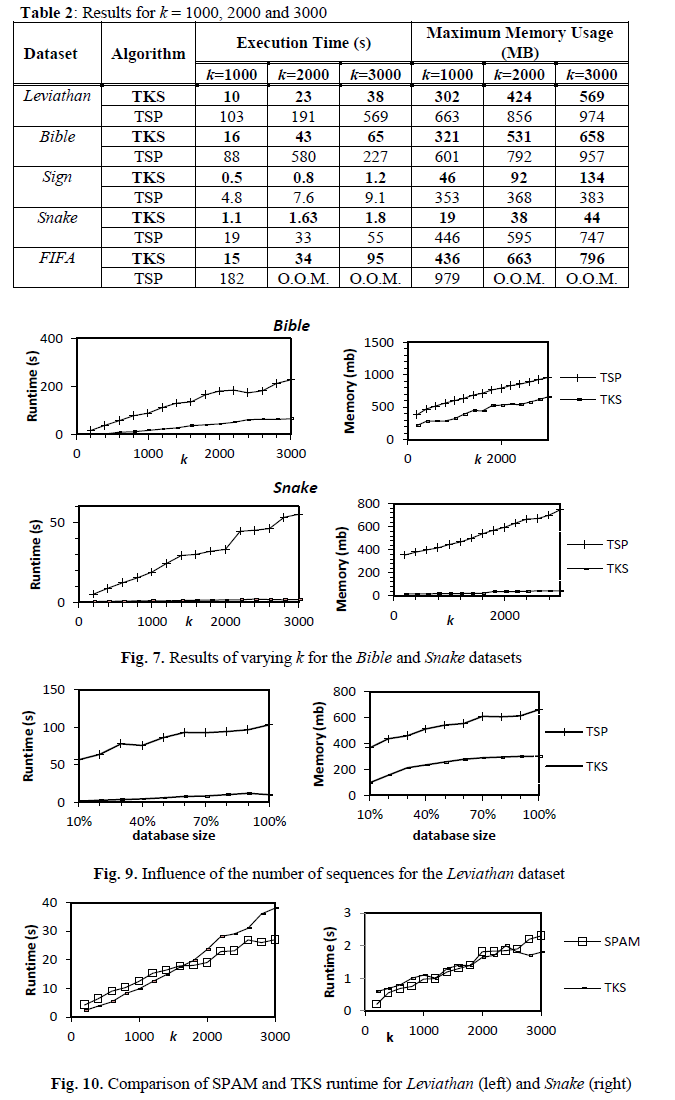
In SPMF 0.95, we have added two new algorithms for discovering top-k sequential patterns named TSP and TKS.

We have performed a comparison of the performance of TSP with TKS for discovering the top-k sequential patterns. Note that the original TSP algorithms discover closed patterns. In our implementation, it discovers all patterns and thus has the same output as TKS.

We have first compared the influence of the k parameter on TKS and TSP. The table below (named Table 2) and the figure below (named Figure 7) show the influence of the k parameter on the execution time and memory usage of TKS and TSP. Results show that TKS has better performance.

We then compared the scalability of TKS and TSP. Results are shown below in the figure named Fig. 9. It shows that TKS and TSP have similar scalability.

We finally compared the performance of TKS with SPAM. This comparison was made because TKS is a SPAM-based algorithm. We wanted to compare TKS with SPAM for the case where SPAM is set with the optimal minsup threshold which is very hard to do in practice. The figure named Fig. 10 below show the results. Its shows that TKS has very closed performance to SPAM. This is good considering that top-k sequential pattern mining is a more difficult problem than mining all patterns with the optimal threshold.

For more details about these results, please refer to the paper about TKS.

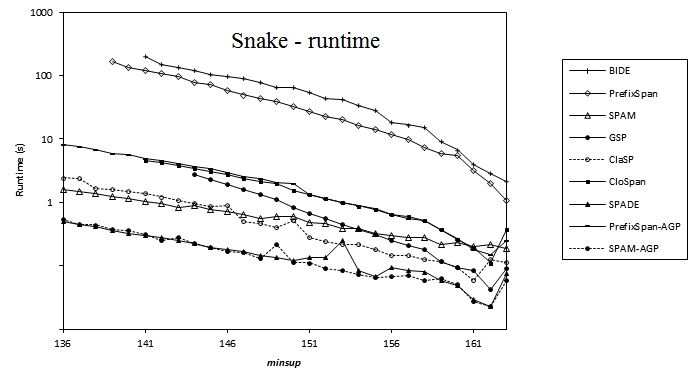
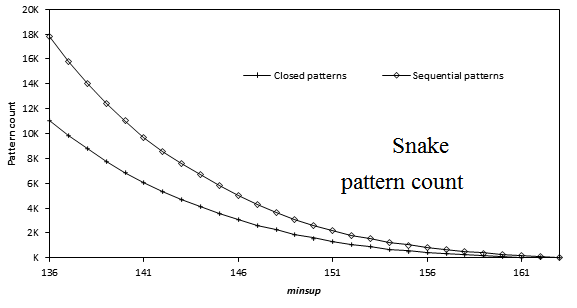
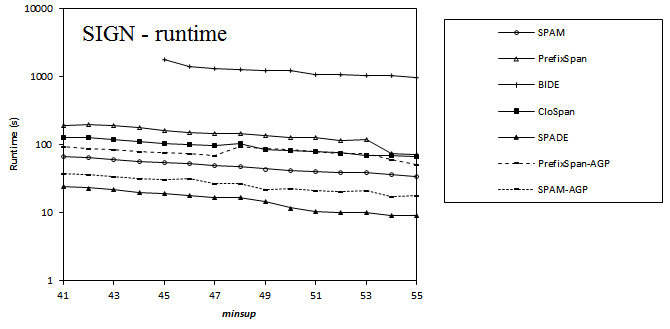
2013-08-14 Performance comparison of sequential pattern mining algorithms (SPMF 0.94)

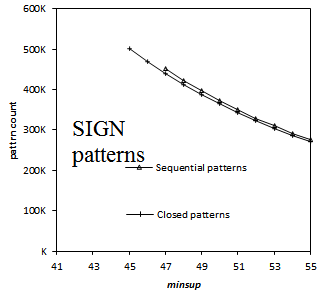
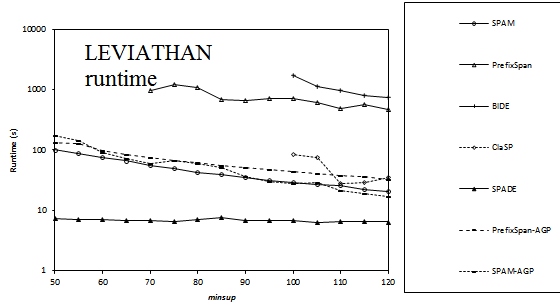
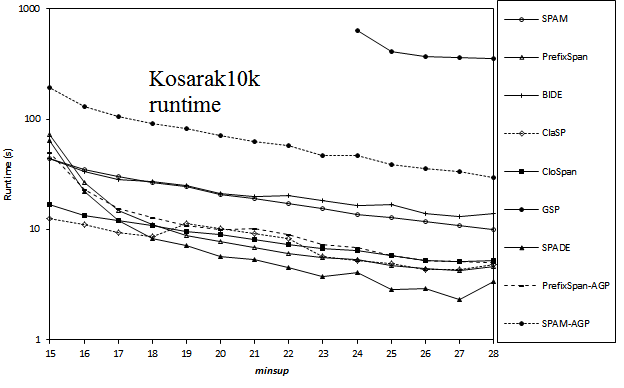
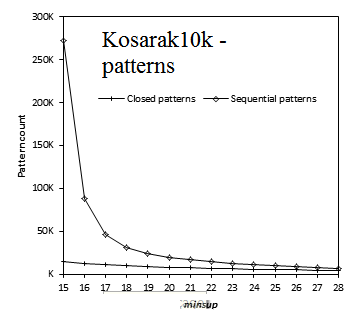
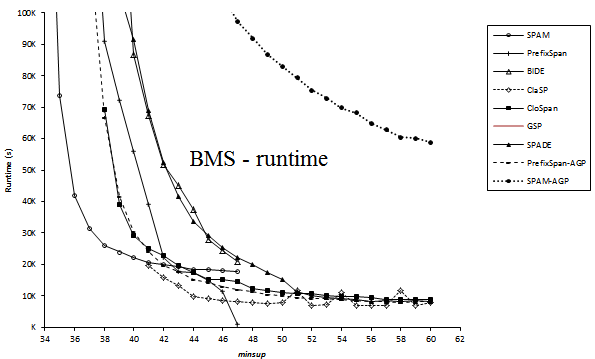
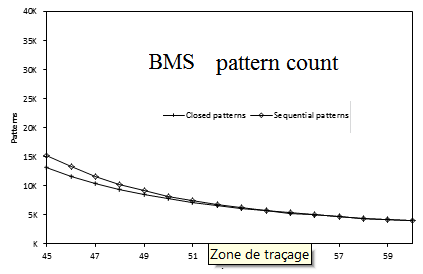
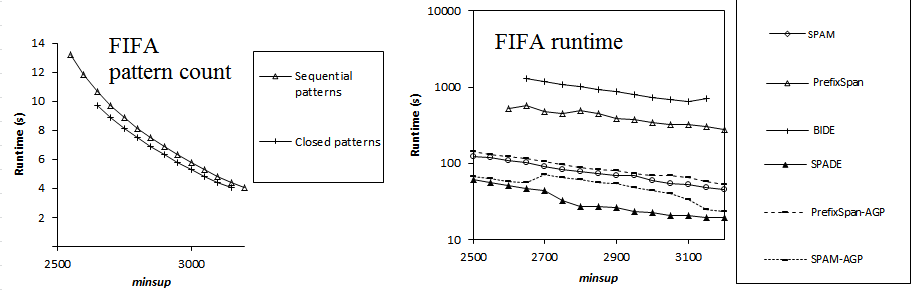
Here is a comparison of the execution time of several sequential pattern mining algorithms offered in SPMF 0.94 on the datasets FIFA, BMS, KOSARAK, SNAKE, SIGN and LEVIATHAN. In these experiments, the minsup parameter is varied. For each dataset, a chart shows the number of closed sequential patterns and the number of sequential patterns with respect to minsup. Furthermore, a chart show the execution time of the various algorithms with respect to minsup. The datasets can be downloaded in the datasets section of this website.

Note 1: that in some charts, some algorithm do not have data points. This is most of time because not enough memory was available on my test computer (it is not because of the algorithm itself).

Note 2: Algorithms in these experiments do not all measure the execution time in the same manner. This can have a slight to moderate influence on the execution time (but should not change the global trend):

• PrefixSpan and BIDE do not count the time of reading the file into RAM.
• SPAM_AGP, GSP, ClaSP, CloSpan and Spade do not count the time of reading the file into RAM and identifying frequent items.
• SPAM counts everything (reading the file, creating a vertical database, eliminating infrequent items, etc.)

For example, for the FIFA dataset, it can make a difference of up to 4 seconds.

Note 3: the BIDE implementation used in this experiment is a slightly improved implementation that will be available in the next version of SPMF (0.95).

The datasets characteristics are:

Dataset	#sequences	# distinct items	avg seq length (items)
FIFA	20450	2990	34.74 (std = 24.08)
LEVIATHAN	5834	9025	33.81 (std= 18.6)
BIBLE	36369	13905	21.64 (std = 12.2)
SIGN	730	267	51.99 (std = 12.3)
SNAKE	163	20	60 (std = 0.59)
BMS	59601	497	2.51 (std = 4.85)
KOSARAK 10K	10000	10094	8.14 (std = 22)

Results for SNAKE:

Results for SIGN:

Results for LEVIATHAN:

Results for KOSARAK10K:

Results for BMS:

Results for FIFA:

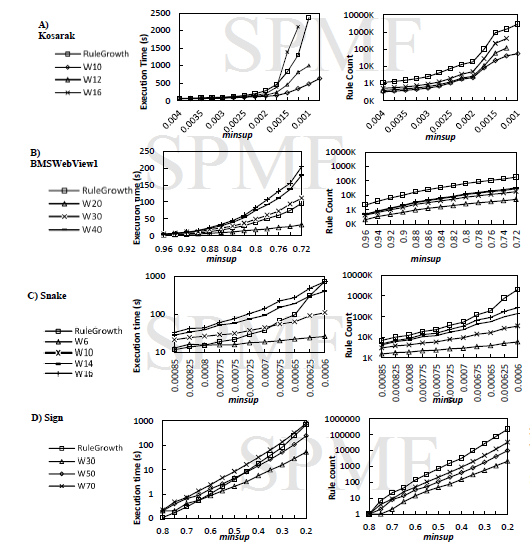
2013-08-12 TRuleGrowth vs. RuleGrowth

Here is a comparison of TRuleGrowth with RuleGrowth for sequential rule mining. The difference between these two algorithms is that TRuleGrowth allows specifying a window size constraint. Below is a performance comparison with four datasets: BMS, Kosarak, SIGN and Snake. In this comparison the notation WX represents TRuleGrowth with a window_size of X consecutive itemsets. As it can be seen in the experiment, using a small window-size can greatly reduce the number of rules found and also decrease the execution time. Using a large window-size however can increase the execution time because extra processing need to be performed for checking the window and the benefits of using a windows are offset.

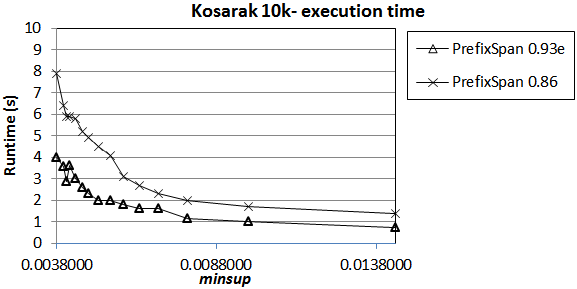
2013-06-17 Performance improvement of PrefixSpan from SPMF 0.86 to SPMF 0.93e

Here is a comparison of the runtime of the PrefixSpan implementation in SPMF 0.93e with the implementation in SPMF 0.86. The goal is to assess the performance improvement resulting of some changes to the data structures, removing some unnecessary code, etc. This experiment was performed on the first 10 000 sequences of the Kosarak dataset. The implementation of SPMF 0.93e seems to be around 50% faster. This was just a quick experiment. More experiments could be done to make a better assessment.

2013-03-31 Which closed itemset mining algorithm is the most efficient?

Here is a comparison of the runtime of Charm, DCI_Closed and AprioriClose for two datasets frequently used in the data mining literature, namely Chess and Mushroom. We have used SPMF v092b.

As we can see AprioriClose (aka AClose) is not very efficient on these two datasets. For Chess, Charm is the most efficient. For Mushroom, DCI_Closed is the most efficient when the minsup parameter is set low. In this experiment, we have not compared the memory usage.

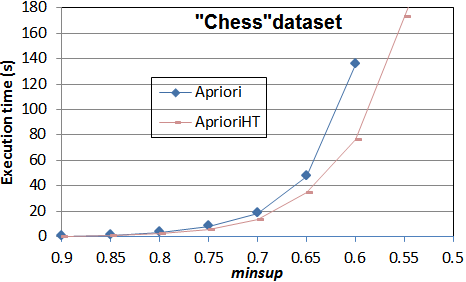
2012-12-29 Implementing Apriori with a hash-tree?

In SPMF 0.91, I have added a version of Apriori called "Apriori_with_hash_tree" ( "AprioriHT") that uses a hash-tree to store candidates. This is an optimization that was proposed in the original paper describing Apriori by Agrawal & Srikant. The advantage is that by storing itemsets in a hash-tree, we can reduce the number of comparisons between candidates and transactions when counting the support of candidates during each iteration. I have done a comparison on the Chess dataset to evaluate the performance gain. The results in terms of execution time are shown below. We can observe that the version with a hash-tree can be almost twice faster for this dataset.

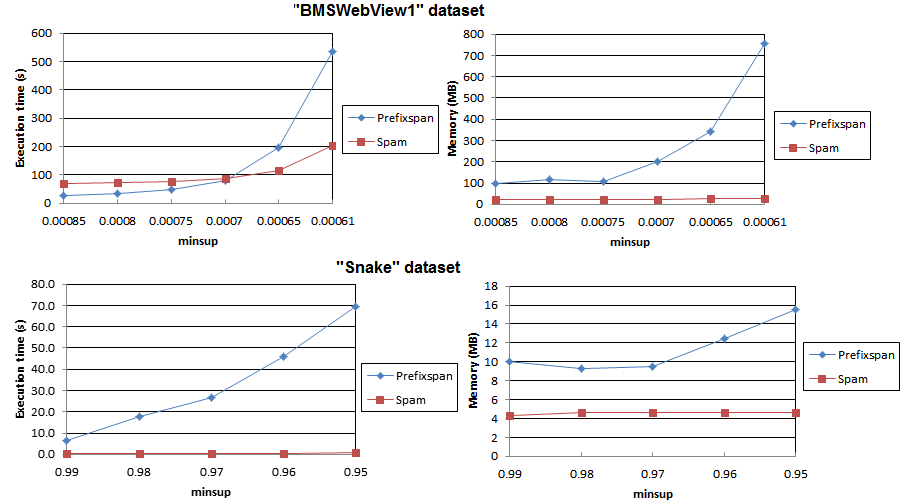
2012-11-28 Which sequential pattern mining algorithm is the most efficient (PrefixSpan vs. SPAM)?

There results are provided by Thomas, Rincy N. (2013). The performance of PrefixSpan and SPAM in SPMF 0.89 are compared on the BMSWebView1 and Snake datasets. The main results are below. As it can be seen SPAM generally have better performance than PrefixSpan on these datasets.

See this paper for more details about this performance comparison:

Thomas, R. N., Yogdhar, P. (2013). Performance Evaluation on State of the Art Sequential Pattern Mining Algorithms. International Journal of Computer Applications. 65(14):8-15, March 2013. Foundation of Computer Science, New York, USA.

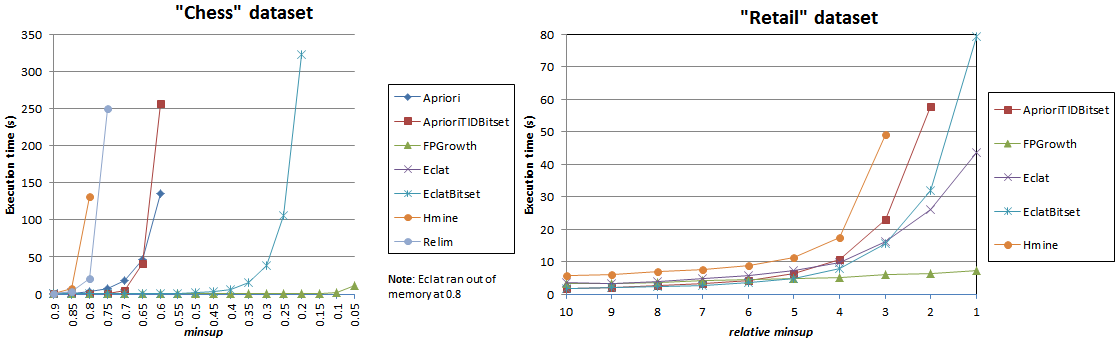
2012-11-13 Which frequent itemset mining algorithm is the most efficient ?

In this experiment, I have compared the execution time of all the frequent itemset mining algorithms that have been implemented in SPMF v0.89 (Apriori, AprioriTID_Bitset, FPGrowth, Eclat, Eclat Bitset, HMine and Relim). I have used the "chess" and "retail" dataset, which are respectively a dense and a sparse dataset. The results are shown below. FPGrowth seems to be clearly the best algorithm both in terms of execution time and memory usage.

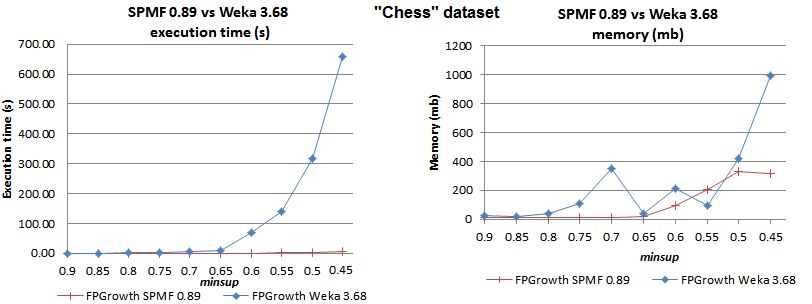
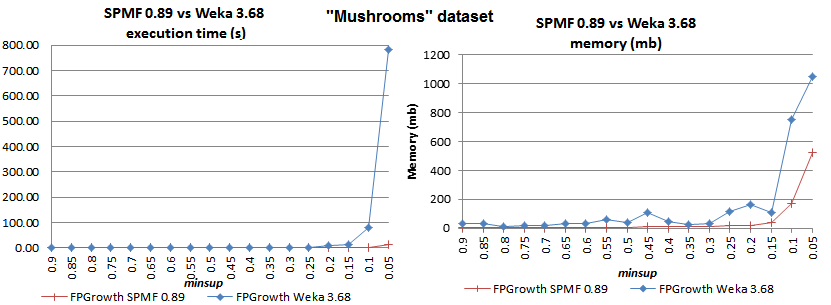
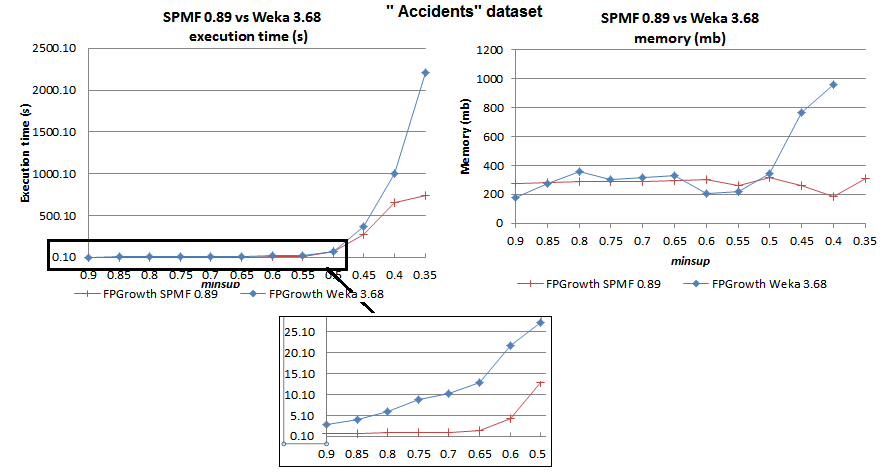
2012-11-12: SPMF vs. Weka: Which implementation of FPGrowth is faster?

We have compared the FPGrowth implementation in SPMF with the implementation provided in the Weka software. In our tests, the SPMF version of FPGrowth is much more efficient. The execution time and memory usage is compared below for the "chess", "mushrooms" and "accidents" datasets, commonly used in the literature.

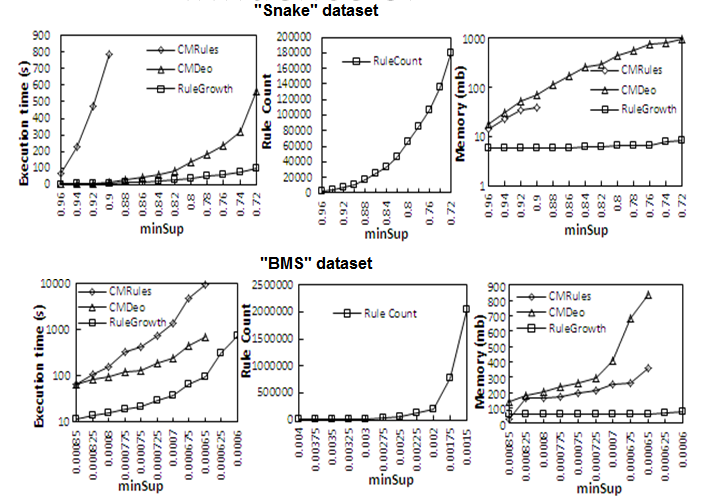
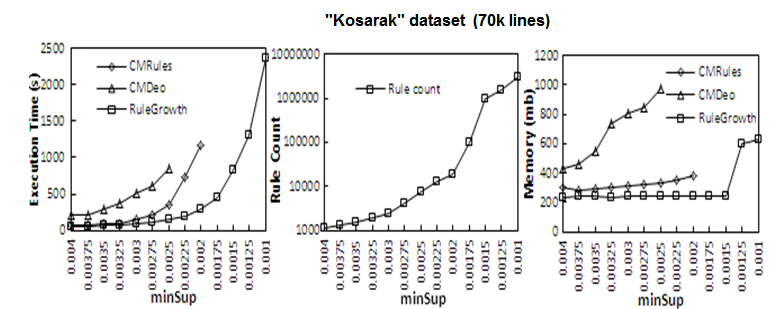
2012-11-10: Which sequential rule mining algorithm is the most efficient ? RuleGrowth, CMRules or CMDeo?

In this experiment, we have compared the performance of three sequential rule mining algorithms. Here are the results of varying the minsup threshold for three datasets (Snake, BMSWebView and Kosarak) with these algorithms. We conclude that RuleGrowth is much more efficient than CMDeo and CMRules.

[If you have performed other experiments with SPMF and you think that they should appear here, please submit them to me by e-mail]